大根堆的创建-java版本
温馨提示：
本文最后更新于 2022年08月28日，已超过 605 天没有更新。若文章内的图片失效（无法正常加载），请留言反馈或直接联系我。
一、介绍
大根堆就是所有父结点都比它的左右孩子大。
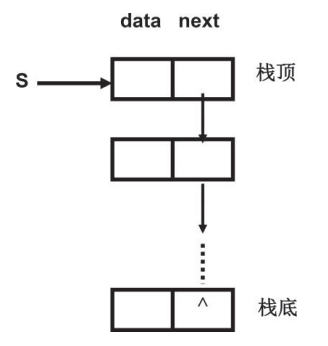
存储结构：采用数组进行存储，同完全二叉树的存储一样。
数组从0开始则：2i+1为左孩子，2i+2为右孩子。
数组从1开始则：2i为左孩子，2i+1为右孩子。
二、算法思想
- 若数组长度为n，根据完全二叉树的性质可知：
（1）1到n/2 为父结点
（2）n/2+1到n为叶子节点 - 叶子结点不需要调整，只需要保证父结点比左右孩子结点大即可。
- 从最后一个父结点向前进行调整，保证每一个父结点比左右孩子大。
- 如果从第一个父结点进行调整无法找到最大的一个结点。
三、算法实现
/**
*
* @param arr
* @param k 需要调整的堆结点
* @param len 数组的长度
*/
void heapAdjust(int arr[],int k,int len) {
int temp = arr[k]; // 暂存需要调整的结点，避免被覆盖
// i指向k的左孩子结点
for(int i = 2*k+1;i <len;i++) {
// i<len保证k有右孩子；同时将i指向较大的一个结点
if(i < len-1 && arr[i]<arr[i+1]) {
i++;
}
// 父节点和孩子结点相同或者父节点大于孩子结点则跳出该次循环
if(arr[i] <= temp) {
break;
} else { // 孩子结点大于父结点则进行调整
arr[k] = arr[i]; // 将孩子结点放到父节点出
k = i; // 父节点重新指向
}
}
arr[k] = temp; // 初始父节点k（arr[0]）找到了合适的位置
}
@Test
public void buildHeap(){
int a[] = {32,45,17,65,53,9,78,87};
System.out.println("原始数组：\n"+Arrays.toString(a));
int len = a.length;
for (int i = len/2 ; i >=0 ; i--) {
heapAdjust(a,i,len);
}
System.out.println("大根堆：\n"+Arrays.toString(a));
}
四、运行结果
正文到此结束
- 本文标签： 数据结构 大根堆
- 本文链接： https://www.it1997.com/article/81
- 版权声明： 本文由小陈没烦恼原创发布，转载请遵循《署名-非商业性使用-相同方式共享 4.0 国际 (CC BY-NC-SA 4.0)》许可协议授权
相关文章
热门推荐
近期评论
-
来自： 好用的截图工具FastStone Capture 带激活码）
-
来自： 留言板
-
来自： 留言板
-
来自： 留言板
-
来自： 留言板